March 18, 2021, by Rupert Knight

Using visual models to solve problems and explore relationships in Mathematics: beyond concrete, pictorial, abstract – Part 1

This two-part blog series by Marc North explores some thinking and strategies for using representations in Mathematics lessons. Part 1 unpicks some of the key theoretical ideas around the use of representations and models and foregrounds how representations can be used to both solve problems and explore mathematical relationships. Part 2 will illustrate these theoretical ideas practically via a classroom based Maths activity.

Our brains don’t like abstract ideas!

There is little doubt that visual models are a key part of the learning and teaching of mathematics. One of the reasons for this is that while much of school mathematics involves abstract concepts that can be generalized across a range of topics and problems, our brains actually don’t like abstract ideas! Instead, many of us prefer to learn and think through concrete examples and deliberately look for concrete and practical examples to help to explain abstract concepts. See, for example, the Learning Scientists site.

Visual models provide a useful tool for ‘concretising’ complex and abstract ideas. The human brain responds positively to information packaged in creative and visual ways, which is why throughout our daily lives we are constantly bombarded with visual imagery and stimuli. It is often easier to remember information presented in picture form than as a string of words, and visual models provide succinct and organised summaries of information. Visual models can also demonstrate relationships between different items and, when shown dynamically, can show how those relationships change and evolve.

Multiple Representations in Teaching for Mastery

The emphasis on a ‘Teaching for Mastery’ approach in both Primary and Secondary schools has ushered in a clear priority for using representations to model and illustrate mathematical ideas and problems. As indicated in Figure 1, the ‘Big Idea’ of representation and structure provides students with access to mathematical concepts and supports them to visualise patterns and make connections both within and between concepts.

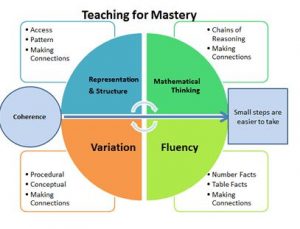
Figure 1: Teaching for Mastery Five Big Ideas (NCETM)

In the Teaching for Mastery approach, the Concrete-Pictorial-Abstract (CPA) framework provides the main approach that structures how teachers are encouraged to work with different representations. The CPA approach is a multi-sensory teaching model that introduces abstract concepts in a concrete and tangible way, by moving from concrete materials, to pictorial representations, to abstract symbols and problems.

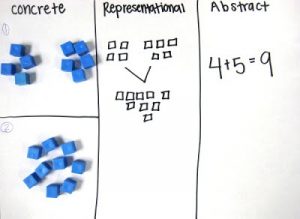
Figure 2: Concrete-Pictorial-Abstract approach (Caroll, Pikul, Foust & Grodziak)

The Concrete dimension is the ‘doing’ stage, where children use physical resources (e.g. manipulatives) to model problems. This stage can also involve the use of concrete situations that are linked to real-life contexts. The Pictorial dimension is the ‘seeing’ stage, where pictures are used to model the concrete resources and the problems. The ‘abstract’ stage is the ‘symbolic’ stage, where abstract mathematical symbols are used to model problems. Many teachers have adopted this approach enthusiastically, operationalizing this practice in various ways:

Figure 3: Varied use of representations to support mathematical learning

Origins of the CPA approach – Bruner’s Representation Modes

The theoretical origins of this approach stem from Jerome Bruner’s work on different representation modes. As a social-constructivist, Bruner argues that children’s problem-solving skills are developed through inquiry and discovery, and also that to support deep learning subject matter should be represented and experienced by children in terms of how they will view and experience the world. This is facilitated by using different representation modes that model the stages of our learning and that reflect the ways in which humans store and encode knowledge and information in memory. The enactive stage (‘based on action’) (from birth to one year old) involves the encoding and storage of information through direct manipulation of objects – for example, think of a baby playing with a rattle. At this early stage, there is no clear internal representation of the object by the individual. The iconic stage (‘based on images’) (from one to six years old) involves an internal representation of external objects visually in the form of a mental image or icon – for example, a child being able to draw a picture of a tree without actually having a tree in front of them. The symbolic stage (‘based on language’) (seven years and up) is when information is able to be stored in the form of a code or symbol – for example, being able to describe a tree in words or through writing.

Potential challenges with the CPA approach

Although the CPA approach is based on Bruner’s work, there are some important distinctions – which also give rise to some potential challenges with this approach.

First, the CPA framework has adopted a theory that describes children’s development and learning through various age ranges into a sequence for instruction for children at all ages. This has resulted in some teachers using this approach in a strictly hierarchical way, always starting with the concrete and progressing to the abstract – and treating the abstract as the ultimate goal of the learning experience in Mathematics. Those students who are not able to demonstrate mastery of the abstract are then deemed to have a lower level of understanding (or no understanding), despite potentially still being able to demonstrate deep understanding wile engaging with concrete and pictorial representations. Some also use the CPA model as a differentiation tool, with lower-attaining students presented with tasks containing mainly concrete and pictorial representations and higher-attaining students encouraged to engage more quickly with abstract elements. Although Bruner’s representation modes are hierarchical in the sense that they map out children’s learning stages through various age ranges, by age 7 years the expectation is that ALL children are capable of creating and storing knowledge at a symbolic level. As such, learning experiences should offer all children opportunities to experience their learning through actions, images, and more formal symbolic means. The sequence in which different representations of knowledge are explored should be determined by the sequence that will lead to the most in-depth understanding of a concept. This could mean working symbolically first, then drawing a picture, then working concretely (e.g. by building a model), or engaging backwards and forwards with each representation mode concurrently while developing and refining understanding – which is precisely what architects and engineers do.

Second, it is problematic to associate the ‘abstract’ stage in the CPA framework exclusively with abstract knowledge and to think that it is only through engagement with formal mathematical symbols and calculations that abstract knowledge is developed. Abstract mathematical structures can also be engaged and represented through enacted activities and pictures or icons. For example, uni-fix cubes are commonly treated as an abstract representation of a concrete object (like apples). Similarly, a bar model inherently contains a degree of abstractness because it shows a standardized or generic model of a unique scenario.

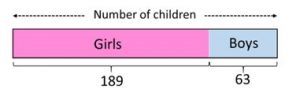
Figure 4: Uni-fix cubes and a bar model – both contain a degree of abstractness

There is a risk, then, that some teachers may not recognise how much abstractness their teaching and resources contain and may wonder why some students continue to be confused despite access to different representations. Encountering formal mathematical structures in enactive or iconic forms does not automatically reduce the degree of abstractness; rather, it merely presents these structures via a medium other than symbols, notation and language.

Although there are numerous classroom resources available that use the CPA approach (for example, see here ), what is less common are resources that help teachers understand which models are the most effective for illustrating certain concepts, why this is, how to build links between different models to support deep relational understanding, and how to use models to compare and contrast different methods. So, while some teachers are using a large number of different representations, they are not always able to give students insight into the decisions behind why specific models are prioritised over others, which makes it difficult for students to know which models to choose when working independently. Also, while models are most commonly used to describe problems and then aid with the solving of those problems, less common is the use of models to compare and contrast different ways of working and to explore mathematical relationships and structures.

It seems important to consider two agenda:

1. the importance of deliberateness when choosing and using models;
2. and, using models to compare and contrast different ways of working and to explore mathematical relationships and structures.

The discussion below draws out some key ideas that have framed these agendas.

Different purposes for mathematics models

While the CPA and Enactive-Iconic-Symbolic frameworks set out different types of models and representations, it is also helpful to think about the different purposes that these can serve. The Realistic Mathematics Education (RME) approach provides some useful thinking around this.
RME, as explained here, was developed in the Netherlands as a specific approach to the teaching of subject Mathematics. This approach has also been used in the United Kingdom with GCSE-resit Mathematics students, as shown here . Three key features of RME are helpful for this discussion:

1. Use of realistic contexts
2. Different purposes for models
3. The ‘progressive formalisation of models’ principle

The first key feature is engagement with abstract mathematics contents in realistic contexts (1), where ‘realistic’ refers to contexts that students can imagine and relate to. The contexts provide an anchor in which to ground understanding of abstract contents, a reference point for structuring thinking about abstract ideas. In part, this reflects some similarity with the ‘concrete’ dimension of the CPA framework.

A second feature of RME is different purposes for working with models (2). ‘Models of’ mathematics are models developed to represent a scenario or problem, with the model bearing a close connection to the problem situation at hand – for example, using a picture of a pizza to represent a fraction of a whole. When (or if) these models are developed and generalised to represent, describe and investigate mathematical structures and relationships over a range of problem situations and even content topics, the model becomes a ‘Model for’ exploring and understanding mathematics. Arrays, bar models and double number-lines are example of models that can be used in this way to describe and investigate mathematical methods, structures and relationships across a range of problem types and situations. ‘Models for’ are powerful precisely because they allow us to investigate mathematical relationships and explore different ways of working.

From a RME perspective, when using representations, it is essential to choose models and representations that can easily be developed from models of a specific local situation to models for describing more general and abstract relationships. This progressive formalisation of models (3) helps students navigate a learning trajectory to abstract concepts and equips them with a small number of models that have applicability over a range of problem and content types.

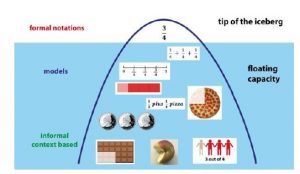
Figure 5: Progressive Formalisation of Models (Hough, Solomon, Dickinson and Gough, 2017)

A key distinction here with the CPA approach is that, from a RME perspective, there is no expectation for students to work through a hierarchy from concrete experiences and pictures to symbolic representations. Instead, the move is from experiences and representations that are bound to local situations towards experiences and representations that are generalizable across a range of situations. The focus is less on the format of the representation and more on how the representation can be molded and developed to explore mathematical relationship and structure.

What does this mean for classroom practice?

The discussion above has attempted to highlight the importance of thinking about both the formats of the representations we use in our teaching AND the purpose of those representations. Using different types of representations that are blended into a deliberate sequence (like the CPA sequence) is helpful for supporting students to think about mathematical concepts from different perspectives – like different pieces of a puzzle, with each piece giving some unique information about the whole picture. However it is also important to think about what we use representation for so that students don’t believe that the only purpose for different representations is to solve problems. A much richer understanding is that representations, when carefully chosen, allow us to explore mathematical relationships, to see connections between mathematical concepts, and – in so doing – to develop a deeper understanding.

Looking ahead to part 2

Part 2 illustrates these theoretical ideas practically via a classroom based Maths activity that explores the relationship between different methods for solving a problem involving a conversion rate (from miles to kilometers). Without giving away too many clues, the key questions that Part 2 explores are:

How are each of these different methods linked, what’s the same and what’s different about them, are there methods that haven’t been considered yet, and what is the most effective ‘model for’ exploring the similarities and differences between them?

Figure 6: Different numerical methods for solving a conversion rate problem

• Share on Facebook
• Share on Twitter
• Share on Google+
• Share on LinkedIn