
January 16, 2018, by Rupert Knight
Mathematics Shanghai style
Three things I learnt from a mathematics lesson study during the Shanghai-England Primary Teacher Exchange
The Exchange
During November, the latest leg of the Shanghai-England primary exchange took place. This is the fourth year of an exchange of primary teachers organised by the Department for Education through local Maths Hubs. In September, two primary teachers from each of the 35 National Maths Hubs had visited Shanghai and then in November the reciprocal visits took place. In this post, Matt Woodford considers some lessons learned from his participation.
As part of the exchange, Maths Hubs organised lesson studies for local practitioners to observe the Shanghai teachers and consider some key messages around teaching for mastery put forward by the NCETM. An example of a previous lesson study event is shown here. I had the privilege of watch a Chinese teacher (Fang) working with a mixed Year 5 and Year 6 class of approximately 30 students. The lesson study took place in a small rural school in Lincolnshire with about 50 teachers watching the lesson. Some academics have pointed out that the success of regions such as Shanghai in the PISA tests are really down to cultural factors. See Jerrim (2015) for a helpful discussion on why East Asian children do so well in PISA tests.
What I value about opportunities like this lesson study is that it allows me to consider what I can learn from Shanghai methods in an English setting. This doesn’t mean that everything they do should be copied – but it should be considered and used to challenge my thinking.
The Lesson
The lesson was the fourth in a series on efficient calculation. The first lesson had covered the commutative law, the second the associative law and the third the distributive law. (I was a little surprised to hear that each topic had been covered in one lesson so was looking forward to seeing the latest lesson in the series!). This fourth lesson required students to put all of that previous information together to find the most efficient ways to calculate answers to problems.
This isn’t going to be an account of the full lesson – as that may take up too much space! So much more happened than is recorded here. It’s also worth saying that the lesson highlighted to me a number of areas that Shanghai teachers can learn from practice in England. However, what I will try to focus on are some of the key ideas that I learnt and have challenged the way I think rather than saying what others should learn.
The opening problem
The lesson began with an opening problem designed to engage students and ascertain initial ideas. The students were asked them to find how many families would live in 25 tower blocks if each had 28 families within it.
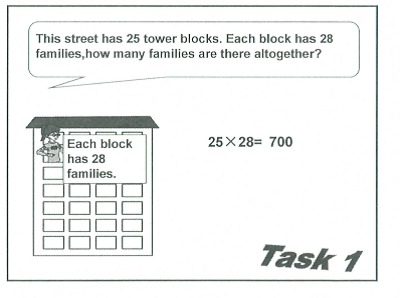
How would you tackle this non-calculator problem? Try to think of a method – then try to think of alternative strategies.
The students I saw agreed a number sentence with their talk partner (of 25 x 28) – then most seemed to suggest a formal, or vertical, method to solve the problem.
The teacher worked through their suggested idea on the adjacent whiteboard before asking students to explain two alternative projected methods.

The first method required the use of the associative law whilst the second method required the distributive law. Both methods have been recreated below and are worth spending the time understanding.
Method 1 Method 2
25 x 28 25 x 28
25 x (4 x 7) 25 x (20 + 8)
25 x 4 x 7 25 x 20 + 25 x 8
100 x 7 500 + 200
700 700
One of things I really enjoyed about the lesson is how the teacher then linked Method 2 with the formal method that many of the students had suggested. This had the twin effects of helping students gain a better understanding of the formal method but also a better understanding of method 2.
Concept clarification
The initial problem was then followed up with an example designed to clarify the concept and help students to follow an argument.
The students were asked to say whether the following working is right or wrong.
808 x 125
(101 x 8) x 125
101 x 125 + 8 x 125
This is a nice example that deliberately tries to expose misunderstandings and root out whether students are learning processes as methods or whether they have a genuine understanding of mathematical structures being used.
Final thoughts: lessons learned
It’s worth stressing again that the message that came out from the day was not that everything that the teachers from Shanghai do is perfect. Fang spoke about how much he had learnt from his English hosts and was in awe of their ability to teach so many subjects. In Shanghai he only teach maths and for only three hours per day. The rest of his time would be spent marking, intervening with students, planning lessons and collaborating with colleagues. The cultural context is very different to what we experience in this country but there are lessons to be considered from his practice.
-
Firstly, notice the care with which the examples have been chosen. 25 x 28 is a really thoughtful choice that works well in illustrating a number of methods. This hasn’t happened by chance. There has been careful consideration about what is the best example to use to allow leaners to make sense of the maths. For example, 24 x 27 would not be nearly as good a choice!
-
This leads to a second key point – whilst mathematical problems in life won’t always be as neat as 25 x 28, the use of these numbers and the exploration of methods allows students to understand mathematical structure. This is particularly important as students will go on to use these same skills in algebra. For example, they will be expected to simplify 3 x 6n or multiply out 2(n + 4). We are part of students’ journeys in making sense of maths. Nothing we do with them is without consequence and what we teach should not just be to get them through this year.
-
Finally, the true/false concept clarification question was a really helpful tool in moving on understanding. This method helps satisfy the key aim of the Maths National Curriculum of developing students’ reasoning skills. Whilst looking at the problem the student I followed first assumed that she must be wrong and that the work on the board must be correct. However, by working with her partner they were able to build the confidence to understand the faulty reasoning.
If you have experiences of working with primary mathematics in a similar way, we would love to read your comments.
Reference
JERRIM, J. 2015. Why do East Asian children perform so well in PISA? An investigation of Western-born children of East Asian descent. Oxford Review of Education, 41, 310-333.
No comments yet, fill out a comment to be the first

Leave a Reply